Einleitung
Eine originale Arbeit mit 46 erreichbaren Punkten zum Thema quadratische Funktionen.
Mit dabei: Linearfaktor, Satz von Vieta, Scheitelpunktsform, Optimierungsproblem und Imbiss Bronko.
39 Minuten Erklärungen in 4 Aufgaben von Koonys Schule.
Aufgaben
Von einer quadratischen Gleichung ist die Lösungsmenge L = $\{\frac{1}{2}; 4\}$ bekannt.
Ermittle mit Hilfe von Linearfaktoren die zugehörige allgemeine quadratische Gleichung.
Wende den Satz von Vieta an, um eine Probe durchzuführen.
Forme in die Scheitelpunktsform um.
Ist der zugehörige Graph durch die Lösungsmenge eindeutig bestimmt?
Beschreibe die Lage der denkbaren Graphen zu der gegebenen Lösungsmenge, wenn zusätzlich vorausgesetzt wird, dass es sich um eine Normalparabel handelt.
Gegeben ist die quadratische Funktion $f$ mit $f(x) = -4x^2 + 20x - 25$.
Bestimme die Nullstellen der Funktion.
Bestimme den Scheitelpunkt der Parabel und stelle fest, ob er der höchste oder tiefste Punkt der Parabel ist.
Welcher Punkt $Q_1$ der Parabel liegt auf der y-Achse?
Welcher Punkt $Q_2$ hat die gleiche 2. Koordinate wie $Q_1$?
Eine Normalparabel geht durch den Ursprung und hat $x = 2$ als Symmetrieachse.
Bestimme den Scheitelpunkt.
Bestimme alle Schnittstellen mit den Koordinatenachsen.
Manuel Romeike hat einen Würstchenstand.
Würstchen werden für 50 Cent das Stück eingekauft und bisher für 2 € das Stück verkauft. Pro Woche werden so 400 Würstchen verkauft.
Für seinen 3-wöchigen Urlaub werden die Aushilfen Tarek, Maxim und Nico eingestellt. Diese drehen in den Wochen von Manuels Abwesenheit am Verkaufspreis der Würstchen. Sie stellen fest, dass mit einer Preisreduzierung um 5 Cent 15 Würstchen mehr pro Woche verkauft werden (z.B. bei 20 Cent 60 Würstchen u.s.w.).
Mit welchem Verkaufspreis würde Manuel am meisten Geld verdienen?
(Löse das Optimierungsproblem systematisch und kommentiere die Arbeitsschritte des Lösungswegs.
Bewerte kurz die Praxistauglichkeit der rechnerischen Lösung. Sollte man nicht lieber gleich 1€ nehmen?)
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
kgV und ggT
50 min, 6 Aufgaben #0010Primfaktorzerlegung, größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches nimmt die Hälfte des Blattes ein. Die andere Hälfte sind Anwendungsaufgaben.
Quadratische Gleichungen
40 min, 5 Aufgaben #0060Die Aufgaben führen schrittweise an das Lösen von reinquadratischen Gleichungen verschiedener Formen heran.
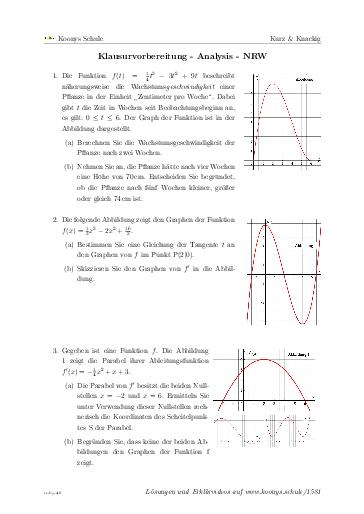
Klausurvorbereitung - Analysis - NRW
16 min, 3 Aufgaben #1581Beispielaufgaben für die zentralen Klausuren aus Nordrhein-Westfalen vom Schulministerium. Es wird vor allem das Verständnis der Ableitungsfunktion geprüft. Wachstumsgeschwindigkeiten, Funktionsgleichungen von Tangenten und Skizzen kommen vor.
Gauß Verfahren
84 min, 7 Aufgaben #1777Für lineare Gleichungssysteme mit mehr als nur zwei Gleichungen und Unbekannten gibt es einen Algorithmus mit dem man bequemer zur Lösung kommt. Dieser wird hier zunächst gezeigt und dann bei Textaufgaben zur Anwendung gebracht.
Abschlussarbeit Klasse 9 mit Taschenrechner
42 min, 6 Aufgaben #2853Aufgaben quer durch die 9. Klasse. Statistiken, lineare Gleichungen, Funktionen, Textgleichungen, Strahlensätze, Prozentrechnung und Flächeninhalten. Auch als Vorbereitung auf den mittleren Schulabschluss (MSA) geeignet.