Prozentrechnung - Grundlagen

Einleitung

Hier geht es um pures Rechnen. Zunächst wird der Zusammenhang von Prozenten und Brüchen geübt und im Anschluss die drei grundlegenden Aufgabentypen der Prozentrechnung.

81 Minuten Erklärungen in 5 Aufgaben von Koonys Schule.

Aufgaben

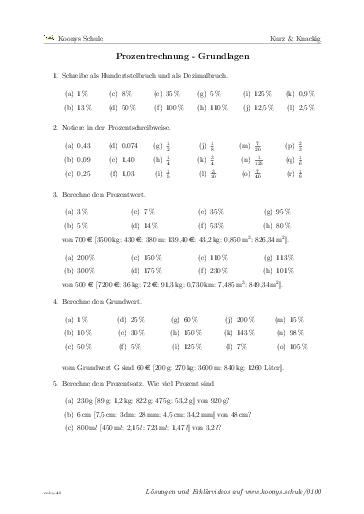
Schreibe als Hundertstelbruch und als Dezimalbruch.

1 %

13 %

8 %

50 %

35 %

100 %

5 %

110 %

125 %

12,5 %

0,9 %

2,5 %

Notiere in der Prozentschreibweise.

0,43

0,09

0,25

0,074

1,40

1,03

$\frac{1}{2}$

$\frac{1}{4}$

$\frac{1}{5}$

$\frac{1}{8}$

$\frac{3}{4}$

$\frac{3}{10}$

$\frac{7}{20}$

$\frac{1}{125}$

$\frac{7}{40}$

$\frac{2}{3}$

$\frac{1}{6}$

$\frac{1}{9}$

Berechne den Prozentwert.

3 %

5 %

7 %

14 %

35 %

53 %

95 %

80 %

von 700€ [3500kg; 430€; 380m; 139,40€; 43,2kg; 0,850$\mathrm{m^3}$; 826,34$\mathrm{m^2}$].

200 %

300 %

150 %

175 %

110 %

230 %

113 %

101 %

von 500€ [7200€; 36kg; 72€; 91,3kg; 0,730km; 7,485$\mathrm{m^3}$; 849,34$\mathrm{m^2}$].

Berechne den Grundwert.

1 %

10 %

50 %

25 %

30 %

5 %

60 %

150 %

125 %

200 %

143 %

7 %

15 %

98 %

105 %

vom Grundwert G sind 60€ [200g; 270kg; 3600m; 840kg; 1260 Liter].

Berechne den Prozentsatz. Wie viel Prozent sind

230g [89g; 1,2kg; 822g; 475g; 53,2g] von 920g?

6cm [7,5cm; 3dm; 28mm; 4,5cm; 34,2mm] von 48cm?

800m$l$ [450m$l$; 2,15$l$; 723m$l$; 1,47$l$] von 3,2$l$?

Alle Erklärungen sind auch in einer Youtube Playlist vorhanden.

Klasse 6 Grundschule Prozentrechnung

PDF zum Drucken

Arbeitsblatt herunterladen

Lösungs-PDF

Lösungen freischalten

Alle Erklärungen sind auch in einer Youtube Playlist vorhanden.

Klasse 6 Grundschule Prozentrechnung

Weitere Arbeitsblätter

Kleine vermischte Übungen - Klasse 8

50 min, 12 Aufgaben #5200

Bunt gemischte Textaufgaben zu verschiedenen Themen der 8. Klasse und darüber hinaus. Etwas zum Knobeln für Schüler am Anfang des Schuljahres.

Klasse 8 Vermischtes

Quadratische Gleichungen

40 min, 5 Aufgaben #0060

Die Aufgaben führen schrittweise an das Lösen von reinquadratischen Gleichungen verschiedener Formen heran.

Klasse 9 Gleichungen

Klausurvorbereitung - Analysis - NRW

15 min, 3 Aufgaben #1580

Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben. Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.

Abitur Analysis

Kegel, Pyramide, Kugel

27 min, 5 Aufgaben #9540

Die Formeln zur Oberflächen- und Volumenberechnung bei Kegeln, Pyramiden und Kugel kommen zur Anwendung. Es kommt dabei u.a. auch der Dreisatz sowie die Dichte-Formel zur Anwendung.

Klasse 10 Körper

Extremwertaufgaben

72 min, 7 Aufgaben #1599

Sieben verschiedene Aufgaben mit immer derselben Fragen: wann wird's maximal bzw. minimal? Sei es ein Rechteck im Kreis, der Graph einer Funktion, eine Konservendose oder eine Marmorplatte: überall muss zuerst eine Hauptbedingung und eine Nebenbedingung aufgestellt und dann zusammen in eine Funktion gepackt werden. Letztlich wird von dieser dann jedes mal der Extrempunkt bestimmt.

Abitur Analysis Leistungskurs

Prozentrechnung - Grundlagen

Einleitung

Aufgaben

PDF zum Drucken

Lösungs-PDF