Einleitung
Der Differenzenquotient muss gebildet und Funktionen abgeleitet werden. Darüber hinaus muss eine Ausgangsfunktion gezeichnet und Funktionsgleichungen von Ausgangsfunktionen gebildet werden.
Eine Aufgabe über die Differenzierbarkeit einer Betragsfunktion an einer bestimmten Stelle ist auch dabei.
34 Minuten Erklärungen in 8 Aufgaben von Koonys Schule.
Aufgaben
Zeigen Sie, dass die Funktion $ f $ mit $ f(x) = x^2 + 2 $ an jeder Stelle ihres Definitionsbereichs differenzierbar ist.
Hinweis: Bilden Sie den Differenzenquotienten an einer beliebigen Stelle $ x_0 $ und bestimmen Sie $ f'(x_0) $.
Bestimmen Sie die Ableitungsfunktion mithilfe der Ableitungsregeln:
$ f(x) = 5x^7 $
$ f(x) = 4x^3 - 3x^2 $
$ f(x) = 0,5x^5 - 2x^3 $
$ f(x) = x^5 + \frac{1}{4}x^4 + \frac{1}{2} x^3 - x $
$ f(x) = ax^2 + bx + c $
$ f(x) = 3x^{20} - 2x^2 $
$ f(x) = \frac{1}{5}(x^2 + x + 5) $
$ f(x) = 2x^2(3x+4) $
Bestimmen Sie die Stellen $ x_i $ an denen die Graphen der Funktionen $ f $ und $ g $ mit $ f(x) = 0,5x^2 - x^3 + 2 $ und $ g(x) = x^3 - 4 $ den gleichen Anstieg haben.
Leiten Sie aus dem dargestellten Graphen der Ableitungsfunktion $ f' $ Aussagen über das Steigungsverhalten der Funktion $ f $ ab.
Welches Verhalten zeigt $ f $ an der Stelle $ x = -2 $?

Bestimmen Sie zu den folgenden Ableitungen von Potenzfunktionen jeweils eine zugehörige Ausgangsfunktion:
$ f'(x) = 4x^3 $
$ f'(x) = 8x^7$
$ f'(x) = 0$
$ f'(t) = 10t^4$
Zeigen Sie, dass die Funktion $ f $ mit $ f(x) = |x|\cdot(1-x) $ an der Stelle $ x = 0 $ nicht differenzierbar ist.
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Wichtige Formeln im Gebäudeenergiegesetz
0 min, 4 Aufgaben #PQUVIn diesem Arbeitsblatt werden die grundlegenden Formeln zur Berechnung der wichtigsten Kennzahlen im Gebäudeenergiegesetz (GEG) vorgestellt. Sie erhalten die notwendigen Formeln und Erklärungen, um den Primärenergiebedarf, den Transmissionswärmeverlust, den Erneuerbare-Energien-Anteil und den U-Wert zu verstehen und anzuwenden. Diese Kennzahlen sind entscheidend für die Beurteilung der Energieeffizienz von Gebäuden und für die Umsetzung der Vorgaben des GEG.
Pythagoras - Anwendungen
49 min, 6 Aufgaben #0040Anwendungsaufgaben mit dem Satz des Pythagoras. Unter anderem werden Diagonale von Quadrat und Würfel berechnet, Berechnungen am gleichschenkligen Dreieck, Pyramide und Walmdach durchgeführt u.v.m.
Klassenarbeit Terme und Gleichungen
27 min, 4 Aufgaben #3749Klassenarbeit einer 8. Klasse auf einem Berliner Gymnasium. Es müssen Terme vereinfacht und Gleichungen gelöst werden. Dabei müssen Klammern aufgelöst, binomische Formeln angewendet und Gleichungen aus Texten aufgestellt werden.
Wochenübung mit Klammern und Gleichungen
29 min, 7 Aufgaben #12347 Aufgaben für 7 Tage. Es müssen Klammern aufgelöst, Terme zusammengefasst und vor allem Gleichungen gelöst werden. Dabei treten unter anderem auch mal Brüche, die binomischen Formeln und die pq-Formel mit auf.
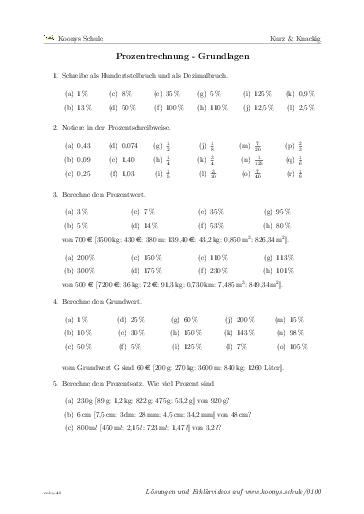
Prozentrechnung - Grundlagen
81 min, 5 Aufgaben #0100Hier geht es um pures Rechnen. Zunächst wird der Zusammenhang von Prozenten und Brüchen geübt und im Anschluss die drei grundlegenden Aufgabentypen der Prozentrechnung.