Einleitung
Anwendungsaufgaben zu Bernoulli-Ketten. Die ersten zwei Aufgaben fragen die grundlegenden Berechnungen ab. Die dritte ist vom Typ mindestens-mindestens und die vierte zeichnet sich durch eine äußert schwierige Aufgabenstellung aus. Ein kühler Kopf ist hier gefragt.
37 Minuten Erklärungen in 4 Aufgaben von Koonys Schule.
Aufgaben
Ein Multiple-Choice Test enthält 19 Fragen mit je 4 Antwortmöglichkeiten von denen jeweils genau eine Antwort richtig ist. Bei 10 richtigen Antworten gilt der Test als bestanden.
Max hat nicht gelernt und fühlt sich nicht gut. Er entscheidet sich dazu alle Antworten zufällig anzukreuzen ohne sich die Fragen durchzulesen, damit er schnell nach Hause kann.
Wie hoch ist die Wahrscheinlichkeit, dass er ...
... besteht?
... durchfällt?
... alles falsch ankreuzt?
... alles richtig ankreuzt?
... mit 10 Punkten besteht?
... mit 9 Punkten durchfällt?
Ein Glücksrad besteht aus 5 gleich großen Sektoren von denen 2 als Treffer gelten und die restlichen als Nieten. Das Glücksrad werde 11 mal gedreht.
Wie hoch ist die Wahrscheinlichkeit, dass ...
... mehr Treffer als Nieten gedreht werden?
... beim letzten mal der 4. Treffer kommt?
... mindestens 2 und höchstens 9 Treffer gedreht werden?
... mehr als 3 Treffer gedreht werden?
... mindestens 3 Treffer gedreht werden?
Wie oft muss man ein Bernoulli-Experiment durchführen, wenn die Wahrscheinlichkeit größer als 72 % sein soll, dass ein Ergebnis der Wahrscheinlichkeit 46 % mindestens einmal eintritt?
Ein Taxistand ist für 10 Taxen vorgesehen. Erfahrungsgemäß hält sich ein Wagen durchschnittlich 12 min pro Stunde am Standplatz auf.
Mit welcher Wahrscheinlichkeit findet eine Taxe bei 3 Standplätzen einen Platz?
Welche Anzahl von Taxen wird am häufigsten am Standplatz anzutreffen sein?
Wie viele Standplätze müssten vorhanden sein, damit mit 90 % Wahrscheinlichkeit stets ein Platz zu finden ist?
Weitere Arbeitsblätter
Übung zu Bewegungen im magnetischem Feld
54 min, 4 Aufgaben #6116Aufgaben mit Elektronen und Protonen, die sich in Magnetfeldern im Kreis bewegen oder abgelenkt werden. Die Lorentzkraft wird dabei der Zentripetalkraft oder der elektrischen Kraft gleichgesetzt.
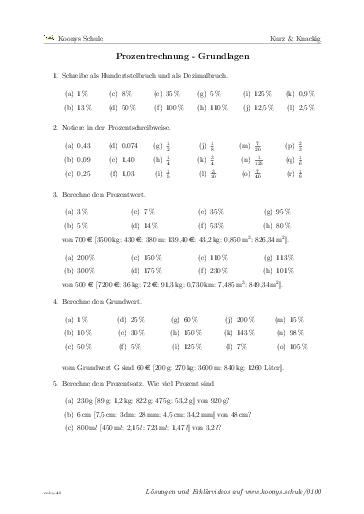
Prozentrechnung - Grundlagen
81 min, 5 Aufgaben #0100Hier geht es um pures Rechnen. Zunächst wird der Zusammenhang von Prozenten und Brüchen geübt und im Anschluss die drei grundlegenden Aufgabentypen der Prozentrechnung.
kgV und ggT
50 min, 6 Aufgaben #0010Primfaktorzerlegung, größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches nimmt die Hälfte des Blattes ein. Die andere Hälfte sind Anwendungsaufgaben.
Übersicht e-Funktionen ableiten
69 min, 7 Aufgaben #6600Schritt für Schritt werden die verschiedenen Ableitungsregeln bei e-Funktionen gezeigt und es gibt Aufgaben mit Kombinationen dieser Regeln (Konstantenregel, Faktorregel, Produktregel, Kettenregel). Das Arbeitsblatt endet mit einer typischen Kurvendiskussion über eine e-Funktion.
Diagnosetest konstruieren und argumentieren
36 min, 5 Aufgaben #4025Aufgaben zur Konstruktion von Dreiecken mit Hilfe der Kongruenzsätze. Außerdem kommen Innenwinkelsatz, ein gleichschenkliges Trapez und die Konstruktion des Umkreises eines Dreiecks im Koordinatensystem vor.