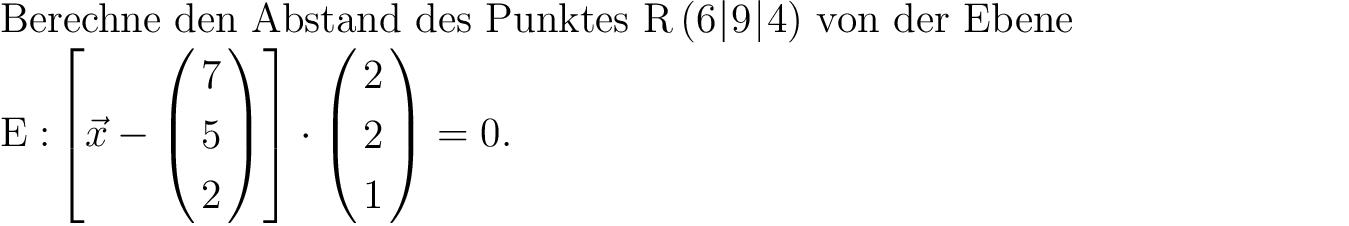Einleitung
Verschiedene Übungen zu Ebenen.
Ebenen mit Spurgeraden zeichnen, Koordinatengleichungen von Ebenen mit verschiedenen Angaben bestimmen, Schnittgeraden, Abstand Punkt Gerade und Verständnisfragen.
52 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
Zeichne die folgenden Ebenen mit Hilfe ihrer Spurgeraden in ein kartesisches Koordinatensystem ein:
E: $3x_1 + 4x_2 + 3x_3 = 12$
E: $2x_1 + 4x_2 = 8$
E: $x_2 = 3$
Bestimme jeweils eine Koordinatengleichung der Ebene E.
$\RPUNKT{A}{2}{2}{2},\, \RPUNKT{B}{4}{1}{3},\,\RPUNKT{C}{8}{4}{5}$
$\RPUNKT{A}{4}{1}{2},\, \mathrm{g:}\,\, \vec{x} = \RVEKTOR{c}{3}{5}{7} + t\cdot \RVEKTOR{c}{1}{1}{1}$
$\mathrm{g:}\,\,\vec{x} = \RVEKTOR{c}{1}{0}{2} + s\cdot \RVEKTOR{c}{3}{1}{2}$, $\mathrm{h:}\,\,\vec{x} = \RVEKTOR{c}{3}{3}{7} + t\cdot \RVEKTOR{c}{2}{1}{3}$
$\mathrm{g:}\,\,\vec{x} = \RVEKTOR{c}{1}{0}{2} + s\cdot \RVEKTOR{c}{3}{1}{2}$, $\mathrm{h:}\,\,\vec{x} = \RVEKTOR{c}{4}{1}{1} + t\cdot \RVEKTOR{c}{6}{2}{4}$
Die Ebene E ist Spiegelebene zwischen $\RPUNKT{A}{1}{4}{7}$ und $\RPUNKT{A^*}{3}{2}{3}$.
Die Ebene E enthält die Gerade $\vec{x} = \RVEKTOR{c}{3}{1}{2} + s \cdot \RVEKTOR{c}{2}{0}{-1}$ und ist orthogonal zur Ebene $\mathrm{F:} - x_1 + x_2 + 2x_3 + 2 = 0$.
Bestimme eine Gleichung der Schnittgeraden der Ebenen $\mathrm{E:} x_1 - x_2 + 2x_3 = 7$ und $\mathrm{F:} -x_1 + x_2 + 2x_3 + 2 = 0$.
Berechne den Abstand des Punktes $\RPUNKT{R}{6}{9}{4}$ von der Ebene
$\mathrm{E:}\left[\vec{x} - \RVEKTOR{c}{7}{5}{2}\right]\cdot \RVEKTOR{c}{2}{2}{1} = 0$.
Gegeben seien die Gerade g und die Ebene E durch $\mathrm{g:}\,\vec{x} = \vec{a} + t\cdot \vec{r},\,\,t\in \RR $ und $\mathrm{E:}\,\left(\vec{x} - \vec{b}\right)\cdot \vec{n} = 0$.
Welche geometrische Bedeutung haben die Vektoren $\vec{a}$, $\vec{b}$, $\vec{r}$, $\vec{n}$ und $\left(\vec{x} - \vec{b}\right)$?
Welche Beziehung muss zwischen den Vektoren gelten, damit gilt
g ist parallel zu E
g ist orthogonal zu E
g liegt in E
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Arbeit - quadratische Funktionen
39 min, 4 Aufgaben #0069Eine originale Arbeit mit 46 erreichbaren Punkten zum Thema quadratische Funktionen. Mit dabei: Linearfaktor, Satz von Vieta, Scheitelpunktsform, Optimierungsproblem und Imbiss Bronko.
Mathematische Kompetenzen - Zufall
15 min, 6 Aufgaben #0008Ein Sachverhalt aus dem Themengebiet Daten und Zufall (Leitidee 5) wird in verschiedene Aufgaben gepackt, die jeweils einen Schwerpunkt bezüglich der mathematischen Kompetenzen besitzen.
Felder und Kreise - GK Klausur Physik
40 min, 3 Aufgaben #6123Originale Physik Klausur für einen Grundkurs im 2. Semester aus Berlin. 39 Punkte, 90min
Strahlensätze **
54 min, 6 Aufgaben #4182Drei Schenkel, verdrehte Skizzen, Erbsen und der Mond sowie Bergspitzen. Das Prinzip ist das Gleiche, aber die Schwierigkeit ist doch um einiges größer als sonst. Das nächste Level an Strahlensatzaufgaben sozusagen.
Textgleichungen mit Brüchen für Profis 1v3
39 min, 8 Aufgaben #1341Textaufgaben müssen gelöst werden indem man Gleichungen aufstellt bei denen Brüche vorkommen.