Einleitung
Klassenarbeit einer 8. Klasse auf einem Berliner Gymnasium.
Es müssen Terme vereinfacht und Gleichungen gelöst werden. Dabei müssen Klammern aufgelöst, binomische Formeln angewendet und Gleichungen aus Texten aufgestellt werden.
26 Minuten Erklärungen in 5 Aufgaben von Koonys Schule.
Aufgaben
Löse, wenn vorhanden, die Klammern auf und fasse die Terme so weit wie möglich zusammen.
$ 3x-y + 15 + 3 - y + 7x - 13 $
$ (25a + 8b) - (3-4a)-(-b) $
$ 8(-3+2r) + 2(4s-r) - 2,5(3s+2) $
$ -2x^2y\cdot (5xyz)\cdot(-0,2z) $
$ \left(4ab^2\right)^2 \cdot bc $
Löse die Gleichungen.
$ 3x + 3 + 5x = 28 + 6x - 11 $
$ -19x - (37 - 15 - 5x - 6) = -5x - 57 + (77+x) $
$ 3(7x - 14) = 4(-9+6x) - 6 $
$ (x+7)^2 = (3-x)^2 $
Ermittle jeweils die gesuchte Zahl, indem Du eine Gleichung aufstellt und diese löst.
Subtrahiert man die gesuchte Zahl von 8, erhält man die S umme von 15,5 und dem Vierfachen der gesuchten Zahl.
Wenn man zur gesuchten Zahl 8 addiert, das Ergebnis versechsfacht und anschließend 33 subtrahiert, erhält man 60.
Gib jeweils zum angegebenen Sachverhalt eine Gleichung mit der Variablen $ x $ für die gesuchte Größe an.
Bestimme die gesuchte Größe.
Klaus und sein Vater haben zusammen ein Alter von 46 Jahren.
Der Vater ist 28 Jahre älter als Klaus.
Gesucht ist das Alter von Klaus.
Ein Blatt Papier ist 6cm länger als breit.
Der Umfang des rechteckigen Blattes ist 50cm.
Gesucht ist die Länge des Blattes.
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Glücksrad mit Urne - Übungsaufgabe Stochastik LK
21 min, 6 Aufgaben #1710Eine Übungsaufgabe, die Urne und Glücksrad kombiniert. Nebst Baumdiagrammen, Bernoulli und der summierten Binomialverteilung werden auch Gewinnerwartung und Prozentrechnung beim Kreis benötigt.
Abzählverfahren
54 min, 7 Aufgaben #1650Aufgaben zur Kombinatorik mit Sitzplätzen, Fußballturnieren, Silvester und defekten Batterien. Man benötigt die Abzählverfahren (mit oder ohne Reihenfolge, mit oder ohne Wiederholung). Das Lotto-Modell und Gewinnerwartung sind auch dabei.
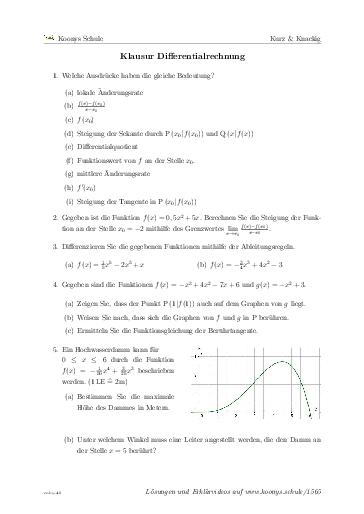
Klausur Differentialrechnung
42 min, 5 Aufgaben #1565Originale Klausur mit 38 Punkten. Das Verständnis zu den Begrifflichkeiten des Themas muss gezeigt, ein Grenzwert mit Hilfe des Differentialquotienten berechnen und Potenzfunktionen mit Ableitungsregeln differenziert (abgeleitet) werden. Zusätzlich kommt das Berührproblem und das Tangentenproblem sowie eine Anwendungsaufgabe vor.
Übersicht e-Funktionen ableiten
69 min, 7 Aufgaben #6600Schritt für Schritt werden die verschiedenen Ableitungsregeln bei e-Funktionen gezeigt und es gibt Aufgaben mit Kombinationen dieser Regeln (Konstantenregel, Faktorregel, Produktregel, Kettenregel). Das Arbeitsblatt endet mit einer typischen Kurvendiskussion über eine e-Funktion.
Kreise - Anwendung
67 min, 6 Aufgaben #8889Flächen- und Umfangsformel des Kreises müssen in verschiedenen Aufgaben flexibel und mehrschrittig eingesetzt werden.