Einleitung
Es werden zunächst quadratische Gleichungen sowohl über die Scheitelpunktsform als auch mit der pq-Formel gelöst. Im Anschluss gibt es Textaufgaben bei denen das Wissen benötigt wird.
74 Minuten Erklärungen in 7 Aufgaben von Koonys Schule.
Aufgaben
Löse die reinquadratischen Gleichungen.
$x^2 = 144$
$4x^2 = 1024$
$x^2+45 = 155,25$
$3x^2-7 = -20$
$5-x^2 = 5$
$7x^2+34=-3x^2+844$
Löse die Gleichungen mit Hilfe der Scheitelpunktsform.
$(x+5)^2 = 64$
$(x-3)^2+2 = 160,76$
$x^2+12x = 3,69$
$x^2+8x+16 = 196$
$x^2-3,6x=0$
$x^2-14x+49 = -50,41$
$3x^2 - 16x=101,97+5x$
$x^2+4x-3=5-3x$
Ermittle die Lösungen mit der pq-Formel.
$x^2-17x+60 = 0$
$2x^2+8x-4,2 = 0$
$x^2+7x-6 = 5-x$
$(x-12)^2 + 22 = 2354$
$x^2-5x+9 = 2x-3$
$4x^2 + 8x-3 = -2x-6x^2+204$
Das Quadrat einer Zahl, vermehrt um das Vierfache dieser Zahl ergibt 21. Für welche Zahlen gilt das?
In einem Rechteck ist die Diagonale d = 20cm. Eine Rechteckseite ist 4cm länger als die andere. Berechne die Länge der Seiten.
Verlängert man alle Seiten eines Quadrates um 4cm, so erhält man die neue Fläche von $1600\mathrm{cm}^2$. Gib die Seitenlängen der beiden Quadrate an.
Verkürzt man eine Seite eines Quadrates um 5cm und verlängert gleichzeitig die andere Seite um 10cm, so erhält man ein Rechteck mit dem Flächeninhalt $154\mathrm{cm}^2$. Berechne die Seitenlängen von Quadrat und Rechteck.
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
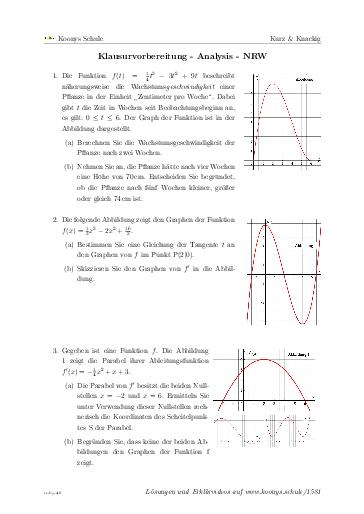
Klausurvorbereitung - Analysis - NRW
16 min, 3 Aufgaben #1581Beispielaufgaben für die zentralen Klausuren aus Nordrhein-Westfalen vom Schulministerium. Es wird vor allem das Verständnis der Ableitungsfunktion geprüft. Wachstumsgeschwindigkeiten, Funktionsgleichungen von Tangenten und Skizzen kommen vor.
Terme vereinfachen
35 min, 4 Aufgaben #2832Übungen zum Vereinfachen von Termen durch die vier Grundrechenarten: Addition, Subtraktion, Multiplikation und Division. Unter anderem müssen gleichartige Glieder zusammengefasst und Klammern aufgelöst werden.
Übungen zu kombinatorischen Abzählverfahren
29 min, 8 Aufgaben #1648Ob mit oder ohne Reihenfolge und mit oder ohne Wiederholung: die Frage, die sich stellt, ist immer die gleiche: wie viele Möglichkeiten gibt es? Bei den Aufgaben kommt man noch häufig durch Abzählen zur Lösung.
Klassenarbeit Terme und Gleichungen
27 min, 4 Aufgaben #3749Klassenarbeit einer 8. Klasse auf einem Berliner Gymnasium. Es müssen Terme vereinfacht und Gleichungen gelöst werden. Dabei müssen Klammern aufgelöst, binomische Formeln angewendet und Gleichungen aus Texten aufgestellt werden.
Bernoulli-Ketten Anwendung
37 min, 4 Aufgaben #1701Anwendungsaufgaben zu Bernoulli-Ketten. Die ersten zwei Aufgaben fragen die grundlegenden Berechnungen ab. Die dritte ist vom Typ mindestens-mindestens und die vierte zeichnet sich durch eine äußert schwierige Aufgabenstellung aus. Ein kühler Kopf ist hier gefragt.